SoH Empirical model

SOH Overview

State of Health estimation is the process of estimating the real performance of a battery post-deployment.This performance metric is an indicator of the remaining useful capacity.

In this document the State of Health (SOH) of the battery is defined as the relative value of its initial charge acceptance vs its actual charge acceptance.

Altergo allows a range of models to be deployed on battery data. These models fall under 4 main categories: Physical, Semi-Empirical, Statistical and Machine Learning and has its own advantages and disadvantages on the basis of parameters like Accuracy, Computational Effort, Adaptability, Dependency on Lab + Field data. These models can be combined to leverage their respective advantages.

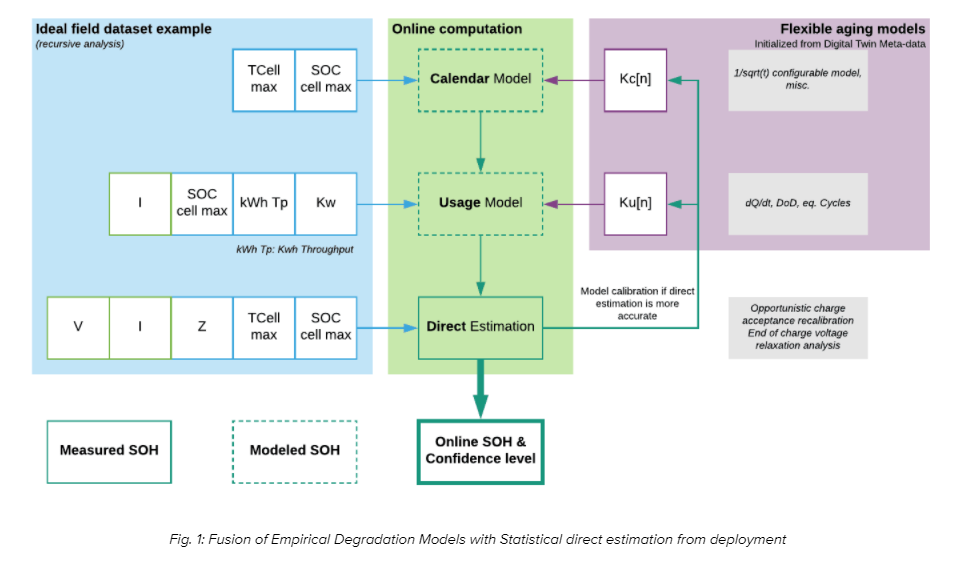
The following example showcases a synergetic use of a Semi-Empirical model and Statistical approach with multiple direct estimation methods.

Semi Empirical SoH

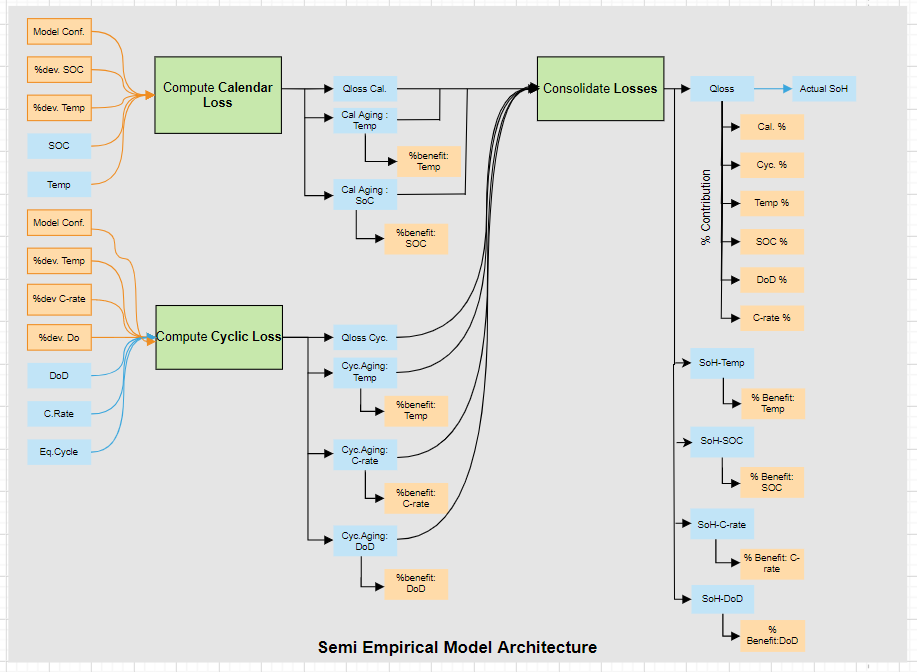
The ageing model uses measurements from the BMS to calculate the SOH. These SoH models have two ageing components accounting for Calendar and Cyclic ageing losses.

Calendar Ageing: Function of resting SoC, Temperature & time. Cal(SoC,T,t)

Cycling Ageing: Function of No. of Equivalent Cycles, Temperature, DoD & Operating C-Rates. Cyc(I,T,DoD,C-Rate)

The Figure mentioned below presents the overall structure of our semi-empirical model. The model is architectured in such a way that the impact of individual ageing factors can be quantified relative to a baseline to help identify clear improvement strategies.

Calendar Ageing

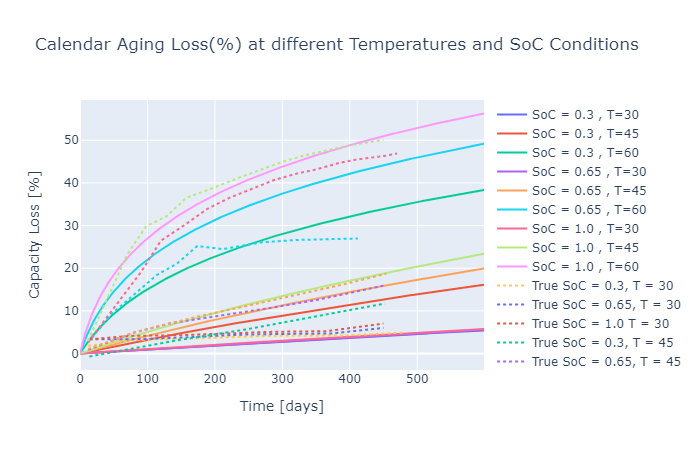
Calendar ageing model is an empirical model which utilises a first-order time-dependent ODE. The calendar ageing model is developed in reference to the model developed in Grolleau et. al. with certain modifications to normalise the output. Temperature is found to be more detrimental than State of Charge (SoC).

Under storage conditions, temperature is commonly taken into account using an Arrhenius law. SoC of storage has minor influence.

Simple empirical expression for predicting capacityfade is proposed as:

$F(x)=\int_{a}^{x} f(t)\,dt$. Then $F$ is continuous, and at all $x$ such that

$\dfrac{dQ_{loss}}{dt} = k(T, SoC) \cdot \left(1+\dfrac{Q_{loss}(t)}{C_{nom}}\right) ^ {-\alpha(T)}$

The above equation solves out as:

$Q_{loss}(t) = \displaystyle -C_{nom} + \left[{C_{nom}}^{\alpha} (\alpha + 1) kt + {C_{nom}}^{\alpha+1}\right]^{\tfrac{1}{(\alpha + 1)}}$

Here,   $\alpha$ is dependent on temperature $T$ and $k$ is dependent on $SoC$ and $T$

k(T,SoC) is the kinetic dependence of the capacity fade evolution with T and SoC during storage, Qloss(t)/Cnom is the fractional capacity loss at aging time t, the term (1 + Qloss(t)/Cnom)$^{-\alpha(T)}$ with ${-\alpha(T)}$ > 0 can be related to the diffusion limitation of solvent molecule inside the SEI layer.

$k$ in the above equation is given by:

$k(T, SoC) = A(T) * SoC + B(T)$

where,

$A(T) = k_A \cdot exp \left[-\dfrac{E_{a_A}}{R} \cdot \left( \dfrac{1}{T} - \dfrac{1}{T_{ref}}\right) \right]$

$B(T) = k_B \cdot exp \left[-\dfrac{E_{a_B}}{R} \cdot \left( \dfrac{1}{T} - \dfrac{1}{T_{ref}}\right) \right]$

Through our assumptions, normalizing the above mentioned equation, hence,

$\dfrac{1}{C_{nom}}\dfrac{dQ_{loss}}{dt} = k(T, SoC) \cdot \left(1+\dfrac{Q_{loss}(t)}{C_{nom}}\right) ^ {-\alpha(T)}$

$\dfrac{Q_{loss}(t)}{C_{nom}} = -1 + (1 + k(\alpha + 1)t)^{\tfrac{1}{\alpha + 1}}$

Here, $k_A$ = 0.293 × 10$^{-5}$ , $E_{a_A}$ = 182 kJ mol$^{-1}$ , $k_B$ = 0.0673 × 10$^{-5}$ , $E_{a_B}$ = 52.1 kJ mol$^{-1}$ are the numerical values of the model parameters, paramater tuning has to be done to adapt for different battery topology.

Figure below shows the calendar ageing model results:

Cyclic Ageing

Cyclic ageing model is an empirical model which takes a number of inputs mentioned above and requires tuning model parameters. The cycle ageing model is developed in reference to the model developed in Wang et. al.

Simple empirical expression for predicting cyclic capacityfade is proposed as:

$Q_{loss} = B \cdot \exp \left( -\dfrac{E_a}{RT}\right)t^z$

Here,

Qloss, is the percentage of capacity loss, B is the pre-exponential factor ( based on Operating C-Rates ), Ea is the activation energy in Jmol−1, R is the gas constant, T is the absolute temperature, and Ah is the Ah-throughput, and z is the power law factor, which is fairly constant for all C-Rates, z = 0.5 which represents a square-root of time dependence with capacity fade due to SEI growth.

Instead of time, Ah-throughput is used as a parameter for life modeling, which is amount of charge delivered by the battery during cycling. Charge throughput is directly proportional to time.

$Ah$ is expressed as : $A_h = full \; capacity * DoD * Cycle \; Number$

The functional form of the life model for different C-Rates and temperatures can be expressed as:

$Q_{loss} = B \cdot \exp \left( \dfrac{-31700 + 370.3 \cdot C_{rate}}{RT}\right)(A_h)^{0.55}$

Model Paramater tuning has to be done to adapt for different battery topology, Certain modifications to use equivalent cycles instead of charge throughput were made in order to normalize the dependency on nominal capacity, thus the generalized model can be expressed as:

$Q_{loss} = B' \cdot \exp \left( \dfrac{-31700 + 370.3 \cdot C_{rate}}{RT}\right)(Eq.Cycles)^{0.55}$

Where Ah transformation is defined as,

$A_h = 2 \cdot C_{nom} \cdot Eq. Cycles$ & $B$ scales by $(2 \cdot C_{nom})^z$ referred as B'

Figure below shows the cyclic ageing model results at different Temperatures:

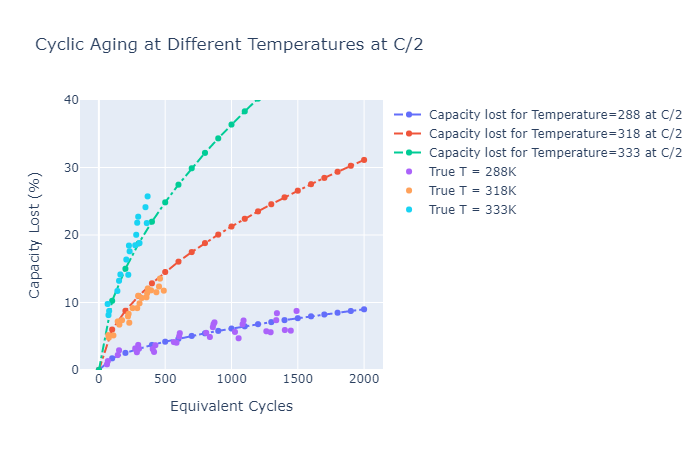
Cyclic Ageing Losses at higher C-Rates and Temperature Conditions:

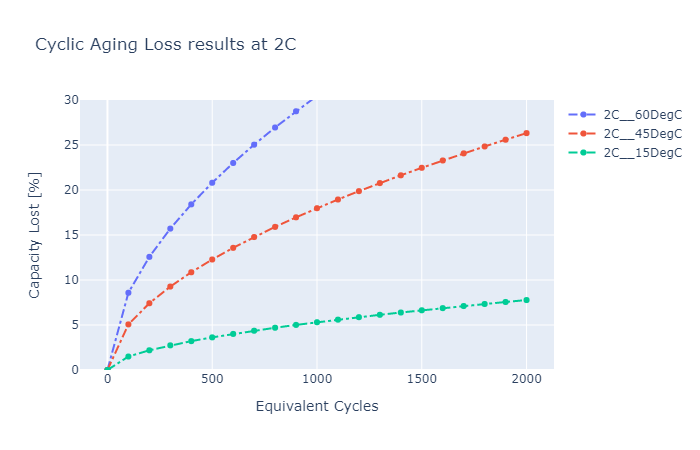
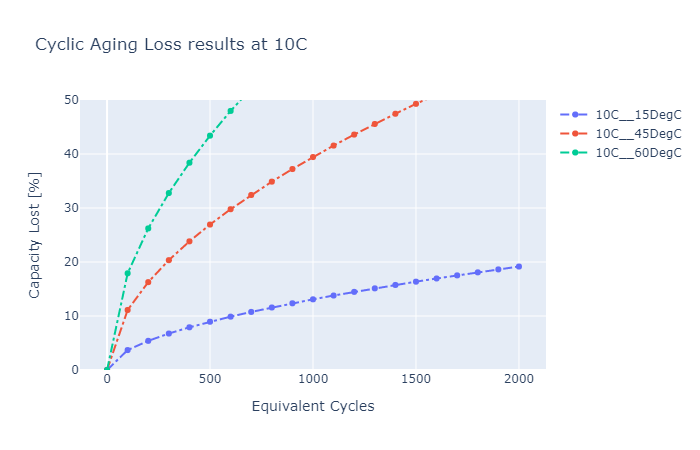
This is a Empirical battery life model that accounts for Ah throughput, time, C-rates, temperature, SoC , Depth of Discharge and achieves qualitative agreement with experimental data. By tuning and configuring model parameters, and adapting battery topological information the model will be able to calculate the most accurate output possible.